David Humen mukaan ihmeisiin ei ole järkevää uskoa, sillä luonnollinen selitys on aina parempi. Vesa Palosen mukaan Humen päättelyssä on todettu vakavia virheitä, ja nyt hän aikoo osoittaa niitä lisää.

Aiemmassa artikkelissani ihmeiden uskottavuudesta kävimme todennäköisyyslaskennan keinoin läpi David Humen väitettä siitä, että ihmeisiin ei pitäisi uskoa. Humehan väitti, että tavallisten tapahtumien suuri määrä riittää kumoamaan suurin piirtein kaikki mahdolliset todisteet epätavallisen tapahtuman puolesta.

Huomasimme, että Hume oli väärässä induktiivisessa päättelyssään yrittäessään päätellä useista tavallisista tapahtumista epätavallisen mahdottomuuden. Lisäksi Hume aliarvioi todistusten tuoman lisän epätavallisen tapahtuman uskottavuudelle. Jo useat Humen aikalaiset, kuten todennäköisyyslaskennan merkittävät kehittäjät Thomas Bayes ja Richard Price, nostivat näitä asioita esiin, mutta aatehistorian virtaukset kulkivat kaikesta huolimatta Humen suuntaan.

Kuten totesimme, ehkä kattavin todennäköisyyslaskennan työkaluja hyödyntävä käsittely Humen ihmeiden vastaisesta argumentista on John Earmanin teos Hume’s Abject Failure: The Argument Against Miracles.

Yksi Uuden testamentin kuuluisimpia ihmeitä, Jeesuksen vetten päällä kävely Julius von Kleverin maalaamana.

Edes Earman ei silti vie tarkasteluaan todistajien vaikutusten kohdalla niin pitkälle kuin se voidaan viedä. Hänen todennäköisyyskäsittelynsä nimittäin olettaa suuren määrän tavallisia tapahtumia, mutta vain todistuksen epätavallisesta tapahtumasta. Hän siis pohtii vain todistusten vaikutusta epätavallisten tapahtumien tapauksessa eikä huomioi sitä, että tavallisista tapahtumista on samoin vain todistuksia. Mikäli todistukset eivät esimerkiksi ole kovin luotettavia, kuten Hume väittää, mistä tiedämme, että epätavallisia tapahtumia ei oikeasti ole jo tapahtunut? Aineistommehan koostuu vain (tavallisten tapahtumien) todistuksista.

Lisäksi Earmanin laskussa joudutaan olettamaan todistukselle jokin luotettavuus.

Kun nämä puutteet korjataan yleisemmässä käsittelyssä, Humen päättelyn ongelmat tulevat yhä ilmeisemmiksi. Kuten pian huomataan, jo yksi todistus riittää tekemään epätavallisesta tapahtumasta uskottavan. Yllättävä tulos johtuu siitä toisaalta siitä, että induktio-päättely monesta tapauksesta jokaiseen tapaukseen on verrattain heikkoa ja toisaalta siitä, että suuri määrä todistuksia vain tavallisista tapahtumista edellyttää todistusten luotettavuutta.

Alla oleva laajempi käsittely pohjaa European Journal for Philosophy of Religion (EJPR) -sarjassa julkaistuun artikkeliini. Artikkelin preprint on saatavilla arxiv-palvelusta.

Realistisempi malli

Pyrimme mahdollisimman neutraaliin käsittelyyn, joten oletamme mahdollisimman vähän ihmeistä ja todellisuuden luonteesta. Analogiana toimikoon uurna, josta vedetään valkoisia ja mustia palloja.

Alla oleva käsittely sisältää jonkin verran todennäköisyyksien pyörittelyä. Matemaattisesti harjaantumaton lukija voi halutessaan ohittaa matemaattiset merkinnät ja keskittyä päättelyn sanalliseen kuvaukseen.

Oletetaan, että meillä on n todistusta joiden mukaan uurnasta vedetty pallo on ollut musta (tavallinen tapahtuma). Luku n voisi olla vaikkapa 100, mutta koska metsästämme yleistä tapausta, merkitsemme määrää muuttujalla n.  Merkitään tätä ‘n todistusta mustan pallon vedosta’-tietoa lyhyesti  \(t(B)^n\) aikaisemman merkintätavan mukaisesti. Meillä on lisäksi yksi todistus siitä, että uurnasta vedetty pallo on valkoinen (ihme), jonka merkkaamme lyhyesti \(t(W)\). Kysymys kuuluu: Mikä on todennäköisyys sille, että tuo yksi pallo todella on ollut valkoinen, kun meillä on tämä yksi todistus valkoisen pallon nostosta ja n todistusta mustien pallojen nostoista aikaisemmin? Eli kuinka suuri on termi \(p(W|t(W)t(B)^n)\)?

Jotta voimme vastata kysymykseen, aiemman jutun käsittelyä täytyy laajentaa hieman. Kuten aiemmin, oletamme etukäteen mahdollisimman vähän uurnan sisällöstä toteamalla, että todennäköisyys v valkoisen pallon vedolle uurnasta (ennen todistuksia) voi olla mitä vain mahdottoman (kaikki pallot mustia) ja välttämättömän (kaikki pallot valkoisia) väliltä. Tämä ilmaistaan niin, että valkoisen pallon todennäköisyys  v on tasaisesti jakautunut nollan ja yhden välillä, lyhyesti merkiten \(v \sim U(0,1)\). Lisäksi oletamme, että korkeintaan yksi viidestä todistuksesta on väärässä, tai tarkemmin, että väärän todistuksen todennäköisyys voi olla mitä vain nollan ja 0.2 väliltä \(d \sim U(0,0.2)\).  Molemmat todennäköisyydet määräytyvät sitten aineiston perusteella todennäköisimpiin arvoihinsa. Näiden edeltä asetettujen todennäköisyyksien eli priorien muodoilla tai ylärajoilla ei siis ole merkittävää vaikutusta tulokseen, kun havaintoja on paljon (n on suuri).

Koska meillä on vain todistuksia pallojen väreille, todennäköisyysmallissa täytyy huomioida myös kunkin pallon oikea väri. Matemaattisesti tämä onnistuu vaikkapa vektorilla \(C^n\) jonka elementit kuvaavat kunkin todistuksen takana olevaa oikeaa väriä. Laskumme on siis otettava huomioon kaikki mahdolliset pallojen oikeat värit todistusten takana, kaikille mahdollisille valkoisten pallojen todennäköisyyksien (v) ja todistusten väärässäolon (d) arvoille. Kaikkien mahdollisuuksien läpikäyntiä kutsutaan todennäköisyyslaskennassa marginalisoinniksi. Käytännössä se tarkoittaa kaikkien mahdollisuuksien \(C^n\) yli summaamista, jatkuvien jakaumien tapauksessa (v ja d) integrointia.

Kokonaistodennäköisyysjakauma tapaukselle on (yksityiskohtaiset laskut artikkelissa)

\[ p( W C^n t(W) t(B)^n v d )=p(v) p(d) p(W|v) p(v) p(t(W) | W d) p(t(B)^n|C^nd) \]

Tästä saadaan todennäköisyyslaskennan kampea kääntämällä kaikki tarvittava, esimerkiksi haluamamme todennäköisyys on

\[ p(W | t(W) t(B)^n)=\frac{p(W t(W) t(B)^n)}{p(t(W) t(B)^n)}=\frac{p(W t(W) t(B)^n)}{p(W t(W) t(B)^n)+p(B t(W) t(B)^n)}, \]

jossa osoittaja saadaan yllämainitulla mahdollisuuksien ylisummauksella

\[ p(W t(W) t(B)^n)=\sum_{∀C^n}\int_0^1dv\int_0^{0.2}dd p(W C^n t(W) t(B)^n v d)=\int_0^1dv\int_0^{0.2}dd v(1-d)(2dv-d-v+1)^n, \]

Nimittäjän toinen termi on vastaavasti

\[ p(B t(W) t(B)^n)=\int_0^1dv\int_0^{0.2}dd (1-v) d (2dv-d-v+1)^n \]

Tuloksia

Todennäköisyys valkoiselle pallolle (ihmeelle) yhden todistuksen perusteella on esitetty kuvassa 1 mustien pallojen (tavallisten tapausten) todistusten määrän n funktiona. Näemme, että kun todistusmäärä mustille palloille kasvaa, valkoisen pallon todennäköisyys yhden todistuksen perusteella lähestyy kaunista arvoa 0.5. Vaikka meillä siis olisi miljardeja todistuksia mustista palloista (tavallisista tapahtumista), jo yksi todistus valkoisesta pallosta riittää nostamaan kyseisen pallon valkoisuuden (ihmeen) todennäköisyyden puolikkaaseen.

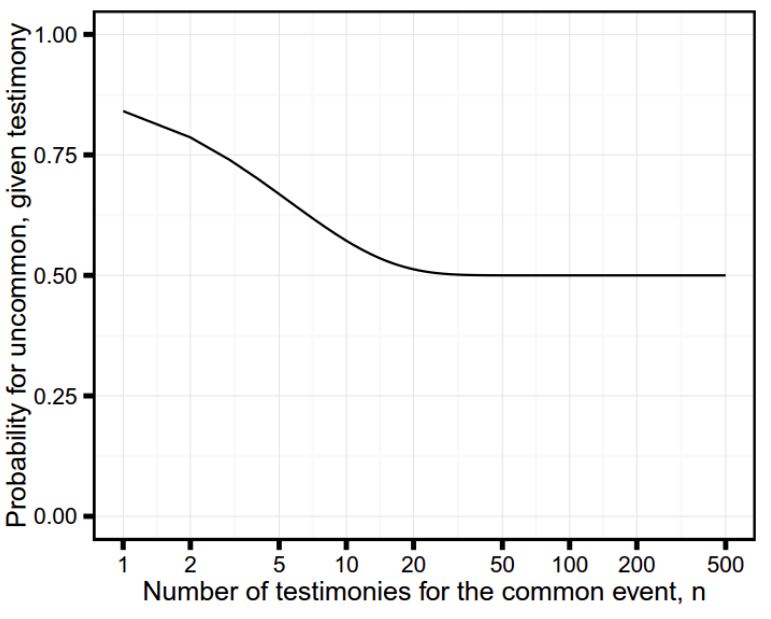
Kuva 1. Todennäköisyys harvinaiselle tapahtumalle W (kun siitä on yksi todistus) tavallisten tapahtumien todistusten t(B) määrän n funktiona.

Tulos voi aluksi tuntua yllättävältä. Todennäköisyyslaskennan koneisto on tässä kuitenkin jäljillä asiasta, jota ei ensi alkuun ehkä tule ajatelleeksi: todistukset ovat rajapintana todellisiin tapahtumiin, joista meillä ei ole suoraa tietoa. Mikäli todistukset eivät ole luotettavia, meillä ei ole merkittävää todistusaineistoa harvinaisia tapahtumia vastaan. Mikäli todistukset taas ovat hyvin luotettavia, myös todistus harvinaisesta tapahtumasta on luotettava (ellei ole riippumatonta syytä epäillä juuri tätä todistusta). Tässä tapauksessa todistus harvinaisesta tapahtumasta riittää vastapainottamaan induktiopäättelystä johtuvan harvinaisen tapahtuman todennäköisyyden pienentymisen. (Aiemmassa jutussa kävimme läpi induktiopäättelyn antaman todennäköisyyden ja sen riippuvuuden n:stä.)

Itse asiassa jotta meillä voisi edes olla hyvin suuri määrä todistuksia vain tavallisista tapahtumista, todistusten täytyy olla hyvin luotettavia. Olisi hyvin epätodennäköistä saada vaikkapa miljoona todistusta vain tavallisista tapahtumista, mikäli todistajat erehtyvät esimerkiksi todennäköisyydellä 0.1.

Laskumme käy läpi kaikki mahdollisuudet mallin puitteissa ja tilanne, joka todennäköisimmin saa aikaan n todistusta tavallisista tapauksista ja yhden todistuksen epätavallisesta tapauksesta on se, että valkoinen pallo todella on harvinainen (v pieni), mutta todistukset ovat luotettavia (d pieni). Harvinaisen tapahtuman todennäköisyys n:n kasvaessa on esitetty kuvassa 2 punaisella ja todistusten väärässä olon todennäköisyys sinisellä. Molemmat pienenevät samaa vauhtia, kun n kasvaa.

Kuva 2. Odotusarvot harvinaisten tapahtumien todennäköisyydelle v (punainen) ja väärille todistuksille d (sininen). Huomaa logaritmiset akselit.

Jos siis olemme kuulleet, että uurnasta on nostettu musta pallo 5000 kertaa, odotamme tämän perusteella luonnollisesti, että mustien pallojen osuus on hyvinkin suuri. Toisaalta se, ettei yhtäkään valkoista palloa ole vieläkään raportoitu, osoittaa, että todistukset ovat hyvin luotettavia: jos virheelliset raportit olisivat yleisiä, osa mustista palloista olisi pitänyt raportoida väärin.
Näin siis todistusten luotettavuus tasapainottaa valkoisten pallojen harvinaisuutta. Kun siis lopulta kuulemme, että uurnasta nostettiin yksi valkoinen pallo, annamme 50% todennäköisyyden sille, että pallo todella oli valkoinen.

Johtopäätöksiä

Yllä oleva analyysi antaa peruslinjauksen harvinaisten tapausten ja ihmeiden analysointiin. Lasku olettaa, että todistukset suuntaan ja toiseen ovat luotettavuudeltaan samaa luokkaa. Tai pikemminkin lasku ei oleta, että todistukset olisivat jotenkin eriarvoisia, koska tämä pitäisi perustella erikseen ja tapahtumafrekvensseistä riippumattomasti. Eritasoiset todistukset (toisen henkilön todistus, oma näköhavainto jne) voitaisiin lisätä malliin lisäämällä useita d:n tyyppisiä parametrejä, jolloin malli monimutkaistuu, mutta tulokset tulevat olemaan samanlaisia.

Perustulos on, että koska tavallisista tapahtumistakin on vain todistuksia, on ihmeeseen rationaalista uskoa jo yhden todistuksen perusteella (tai olla uskomatta, mutta todennäköisyys on 0.5), vaikka todistuksia tavallisista tapahtumista olisi kuinka paljon. Ihmetodistuksen epäilyyn tarvitaan muita perusteluja kuin tuntuma siitä, että harvinaisia tapahtumia (ihmeitä) ei vain tapahdu, koska niitä ei ole ennen havaittu. (Lasku ottaa tämän mahdollisuuden jo huomioon ja osoittaa päättelyn vääräksi.)

Sarjan kolmannessa osassa on tarkoitus käsitellä tapausta, jossa harvinaisille tapahtumille (ihmeille) on tunnettuja vääriä todistuksia. Innokkaimmat voivat jo katsoa tapauksen käsittelyn arxiv-paperista.

Kirjoitus pohjautuu artikkeliin “A Bayesian Baseline for Belief in Uncommon Events” European Journal for Philosophy of Religion -lehdessä.

Jos pidit lukemastasi, tykkää Areiopagista Facebookissa, seuraa Twitterissä ja tilaa kirjoitukset sähköpostiisi.

Kuva 1: Wikimedia Commons. PD.

Kuva 2: Wikimiedia Commons. PD.